Misplaced Pages

In optics, a dispersive prism is an optical prism that is used to disperse light, that is, to separate light into its spectral components (the colors of the rainbow). Different wavelengths (colors) of light will be deflected by the prism at different angles. This is a result of the prism material's index of refraction varying with wavelength (dispersion). Generally, longer wavelengths (red) undergo a smaller deviation than shorter wavelengths (blue). The dispersion of white light into colors by a prism led Sir Isaac Newton to conclude that white light consisted of a mixture of different colors.

Triangular prisms are the most common type of dispersive prism. Other types of dispersive prism exist that have more than two optical interfaces; some of them combine refraction with total internal reflection.

Principle

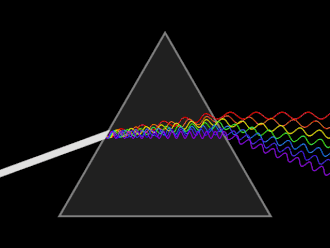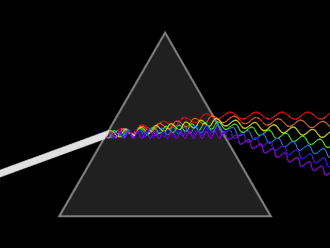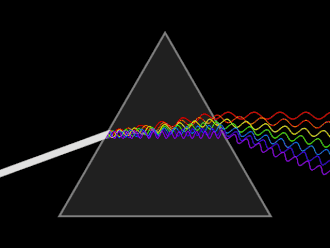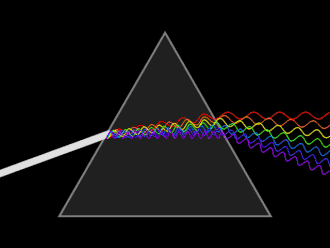
Light changes speed as it moves from one medium to another (for example, from air into the glass of the prism). This speed change causes the light to be refracted and to enter the new medium at a different angle (Huygens principle). The degree of bending of the light's path depends on the angle that the incident beam of light makes with the surface, and on the ratio between the refractive indices of the two media (Snell's law). The refractive index of many materials (such as glass) varies with the wavelength or color of the light used, a phenomenon known as dispersion. This causes light of different colors to be refracted differently and to leave the prism at different angles, creating an effect similar to a rainbow. This can be used to separate a beam of white light into its constituent spectrum of colors.

Prisms will generally disperse light over a much larger frequency bandwidth than diffraction gratings, making them useful for broad-spectrum spectroscopy. Furthermore, prisms do not suffer from complications arising from overlapping spectral orders, which all gratings have. A usual disadvantage of prisms is lower dispersion than a well-chosen grating can achieve.

Prisms are sometimes used for the internal reflection at the surfaces rather than for dispersion. If light inside the prism hits one of the surfaces at a sufficiently steep angle, total internal reflection occurs and all of the light is reflected. This makes a prism a useful substitute for a mirror in some situations.

Types

• Triangular prism
• Amici prism and other types of compound prisms
• Littrow prism with mirror on its rear facet
• Pellin–Broca prism
• Abbe prism
• Féry prism

Deviation angle and dispersion

Thick prism

Ray angle deviation and dispersion through a prism can be determined by tracing a sample ray through the element and using Snell's law at each interface. For the prism shown at right, the indicated angles are given by

${\displaystyle {\begin{aligned}\theta '_{0}&=\,{\text{arcsin}}{\Big (}{\frac {n_{0}}{n_{1}}}\,\sin \theta _{0}{\Big )}\\\theta _{1}&=\alpha -\theta '_{0}\\\theta '_{1}&=\,{\text{arcsin}}{\Big (}{\frac {n_{1}}{n_{2}}}\,\sin \theta _{1}{\Big )}\\\theta _{2}&=\theta '_{1}-\alpha \end{aligned}}}$.

All angles are positive in the direction shown in the image. For a prism in air ${\displaystyle n_{0}=n_{2}\simeq 1}$. Defining ${\displaystyle n=n_{1}}$, the deviation angle ${\displaystyle \delta }$ is given by

${\displaystyle \delta =\theta _{0}+\theta _{2}=\theta _{0}+{\text{arcsin}}{\Big (}n\,\sin {\Big }{\Big )}-\alpha }$

Thin prism approximation

If the angle of incidence ${\displaystyle \theta _{0}}$ and prism apex angle ${\displaystyle \alpha }$ are both small, ${\displaystyle \sin \theta \approx \theta }$ and ${\displaystyle {\text{arcsin}}x\approx x}$ if the angles are expressed in radians. This allows the nonlinear equation in the deviation angle ${\displaystyle \delta }$ to be approximated by

${\displaystyle \delta \approx \theta _{0}-\alpha +{\Big (}n\,{\Big }{\Big )}=\theta _{0}-\alpha +n\alpha -\theta _{0}=(n-1)\alpha \ .}$

The deviation angle depends on wavelength through n, so for a thin prism the deviation angle varies with wavelength according to

${\displaystyle \delta (\lambda )\approx \alpha }$.

Multiple prisms

Aligning multiple prisms in series can enhance the dispersion greatly, or vice versa, allow beam manipulation with suppressed dispersion.

As shown above, the dispersive behaviour of each prism depends strongly on the angle of incidence, which is determined by the presence of surrounding prisms. Therefore, the resulting dispersion is not a simple sum of individual contributions (unless all prisms can be approximated as thin ones).

Choice of optical material for optimum dispersion

Although the refractive index is dependent on the wavelength in every material, some materials have a much more powerful wavelength dependence (are much more dispersive) than others. Unfortunately, high-dispersion regions tend to be spectrally close to regions where the material becomes opaque.

Crown glasses such as BK7 have a relatively small dispersion (and can be used roughly between 330 and 2500 nm), while flint glasses have a much stronger dispersion for visible light and hence are more suitable for use as dispersive prisms, but their absorption sets on already around 390 nm. Fused quartz, sodium chloride and other optical materials are used at ultraviolet and infrared wavelengths where normal glasses become opaque.

The top angle of the prism (the angle of the edge between the input and output faces) can be widened to increase the spectral dispersion. However it is often chosen so that both the incoming and outgoing light rays hit the surface at around the Brewster angle; beyond the Brewster angle reflection losses increase greatly and angle of view is reduced. Most frequently, dispersive prisms are equilateral (apex angle of 60 degrees).

History

Like many basic geometric terms, the word prism (Greek: πρίσμα, romanized: prisma, lit. 'something sawed') was first used in Euclid's Elements. Euclid defined the term in Book XI as "a solid figure contained by two opposite, equal and parallel planes, while the rest are parallelograms", however the nine subsequent propositions that used the term included examples of triangular-based prisms (i.e. with sides which were not parallelograms). This inconsistency caused confusion amongst later geometricians.

René Descartes had seen light separated into the colors of the rainbow by glass or water, though the source of the color was unknown. Isaac Newton's 1666 experiment of bending white light through a prism demonstrated that all the colors already existed in the light, with different color "corpuscles" fanning out and traveling with different speeds through the prism. It was only later that Young and Fresnel combined Newton's particle theory with Huygens' wave theory to explain how color arises from the spectrum of light.

Newton arrived at his conclusion by passing the red color from one prism through a second prism and found the color unchanged. From this, he concluded that the colors must already be present in the incoming light – thus, the prism did not create colors, but merely separated colors that are already there. He also used a lens and a second prism to recompose the spectrum back into white light. This experiment has become a classic example of the methodology introduced during the scientific revolution. The results of the experiment dramatically transformed the field of metaphysics, leading to John Locke's primary vs secondary quality distinction.

Newton discussed prism dispersion in great detail in his book Opticks. He also introduced the use of more than one prism to control dispersion. Newton's description of his experiments on prism dispersion was qualitative. A quantitative description of multiple-prism dispersion was not needed until multiple prism laser beam expanders were introduced in the 1980s.

Grisms (grating prisms)

A diffraction grating may be ruled onto one face of a prism to form an element called a "grism". Spectrographs are extensively used in astronomy to observe the spectra of stars and other astronomical objects. Insertion of a grism in the collimated beam of an astronomical imager transforms that camera into a spectrometer, since the beam still continues in approximately the same direction when passing through it. The deflection of the prism is constrained to exactly cancel the deflection due to the diffraction grating at the spectrometer's central wavelength.

A different sort of spectrometer component called an immersed grating also consists of a prism with a diffraction grating ruled on one surface. However, in this case the grating is used in reflection, with light hitting the grating from inside the prism before being totally internally reflected back into the prism (and leaving from a different face). The reduction of the light's wavelength inside the prism results in an increase of the resulting spectral resolution by the ratio of the prism's refractive index to that of air.

With either a grism or immersed grating, the primary source of spectral dispersion is the grating. Any effect due to chromatic dispersion from the prism itself is incidental, as opposed to actual prism-based spectrometers.

In popular culture

An artist's rendition of a dispersive prism is seen on the cover of Pink Floyd's The Dark Side of the Moon, one of the best-selling albums of all time. Somewhat unrealistically, the iconic graphic shows a divergent ray of white light passing the prism, separating into its spectrum only after leaving the prism's rear facet.

See also

• Optical spectroscopy
• Monochromator
• Multiple-prism dispersion theory
• Multiple-prism grating laser oscillator

References

1. M. Born and E. Wolf, Principles of Optics, 7 ed. (Cambridge University, Cambridge, 1999), pp. 190–193.
2. Elements: book 11, Def 13 and Prop 28, 29, 39; and book 12, Prop 3, 4, 5, 7, 8, 10
3. Thomas Malton (1774). A Royal Road to Geometry: Or, an Easy and Familiar Introduction to the Mathematics. ... By Thomas Malton. ... author, and sold. pp. 360–.
4. James Elliot (1845). Key to the Complete Treatise on Practical Geometry and Mensuration: Containing Full Demonstrations of the Rules ... Longman, Brown, Green, and Longmans. pp. 3–.
5. James Gleick (8 June 2004). Isaac Newton. Vintage. ISBN 1400032954.
6. Isaac Newton (1704). Opticks. London: Royal Society. ISBN 0-486-60205-2.
7. "Colours of two kinds - Physics narrative". Institute of Physics. Retrieved 13 April 2021.
8. F. J. Duarte and J. A. Piper (1982). "Dispersion theory of multiple-prism beam expanders for pulsed dye lasers". Opt. Commun. 43 (5): 303–307. Bibcode:1982OptCo..43..303D. doi:10.1016/0030-4018(82)90216-4.

• Prisms (optics)