| This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed. Find sources: "Milliradian" – news · newspapers · books · scholar · JSTOR (April 2021) (Learn how and when to remove this message) |
| Milliradian | |
|---|---|
 The PSO-1 reticle in a Dragunov sniper rifle has markings with 1-mrad spacing, which can be used to compensate for wind drift, impact correction or range estimation. The PSO-1 reticle in a Dragunov sniper rifle has markings with 1-mrad spacing, which can be used to compensate for wind drift, impact correction or range estimation. | |
| General information | |
| Unit system | SI derived unit |
| Unit of | Angle |
| Symbol | mrad, mil |
| Named after | The metric prefix milli- (from Latin mille meaning "one thousand") and the radian |
| In units | Dimensionless with an arc length one thousandth of the radius, i.e. 1 mm/m or 1 m/km |
| Conversions | |
| 1 mrad in ... | ... is equal to ... |
| radians | 1/1000 rad |
| turns | 1/2000π turn |
| gradians | 1/5π ≈ 0.063662 |
| degrees | 9/50π ≈ 0.057296° |
| arcminutes | 54/5π ≈ 3.4377′ |
A milliradian (SI-symbol mrad, sometimes also abbreviated mil) is an SI derived unit for angular measurement which is defined as a thousandth of a radian (0.001 radian). Milliradians are used in adjustment of firearm sights by adjusting the angle of the sight compared to the barrel (up, down, left, or right). Milliradians are also used for comparing shot groupings, or to compare the difficulty of hitting different sized shooting targets at different distances. When using a scope with both mrad adjustment and a reticle with mrad markings (called an "mrad/mrad scope"), the shooter can use the reticle as a ruler to count the number of mrads a shot was off-target, which directly translates to the sight adjustment needed to hit the target with a follow-up shot. Optics with mrad markings in the reticle can also be used to make a range estimation of a known size target, or vice versa, to determine a target size if the distance is known, a practice called "milling".
Milliradians are generally used for very small angles, which allows for very accurate mathematical approximations to more easily calculate with direct proportions, back and forth between the angular separation observed in an optic, linear subtension on target, and range. In such applications it is useful to use a unit for target size that is a thousandth of the unit for range, for instance by using the metric units millimeters for target size and meters for range. This coincides with the definition of the milliradian where the arc length is defined as 1/1,000 of the radius. A common adjustment value in firearm sights is 1 cm at 100 meters which equals 10 mm/100 m = 1/10 mrad.
The true definition of a milliradian is based on a unit circle with a radius of one and an arc divided into 1,000 mrad per radian, hence 2,000 π or approximately 6,283.185 milliradians in one turn, and rifle scope adjustments and reticles are calibrated to this definition. There are also other definitions used for land mapping and artillery which are rounded to more easily be divided into smaller parts for use with compasses, which are then often referred to as "mils", "lines", or similar. For instance there are artillery sights and compasses with 6,400 NATO mils, 6,000 Warsaw Pact mils or 6,300 Swedish "streck" per turn instead of 360° or 2π radians, achieving higher resolution than a 360° compass while also being easier to divide into parts than if true milliradians were used.
History

The milliradian (approximately 6,283.185 in a circle) was first used in the mid-19th century by Charles-Marc Dapples (1837–1920), a Swiss engineer and professor at the University of Lausanne. Degrees and minutes were the usual units of angular measurement but others were being proposed, with "grads" (400 gradians in a circle) under various names having considerable popularity in much of northern Europe. However, Imperial Russia used a different approach, dividing a circle into equilateral triangles (60° per triangle, 6 triangles in a circle) and hence 600 units to a circle.
Around the time of the start of World War I, France was experimenting with the use of millièmes or angular mils (6400 in a circle) for use with artillery sights instead of decigrades (4000 in a circle). The United Kingdom was also trialing them to replace degrees and minutes. They were adopted by France although decigrades also remained in use throughout World War I. Other nations also used decigrades. The United States, which copied many French artillery practices, adopted angular mils, later known as NATO mils. Before 2007 the Swedish defence forces used "streck" (6300 in a circle, streck meaning lines or marks) (together with degrees for some navigation) which is closer to the milliradian but then changed to NATO mils. After the Bolshevik Revolution and the adoption of the metric system of measurement (e.g. artillery replaced "units of base" with meters) the Red Army expanded the 600 unit circle into a 6000 mil circle. Hence the Russian mil has a somewhat different origin than those derived from French artillery practices.
In the 1950s, NATO adopted metric units of measurement for land and general use. NATO mils, meters, and kilograms became standard, although degrees remained in use for naval and air purposes, reflecting civil practices.
Mathematical principle

 Left: An angle of 1 radian (marked green, approximately 57.3°) corresponds to an angle where the length of the arc (blue) is equal to the radius of the circle (red).
Left: An angle of 1 radian (marked green, approximately 57.3°) corresponds to an angle where the length of the arc (blue) is equal to the radius of the circle (red).Right: A milliradian corresponds to 1/1000 of the angle of a radian. (The image on the right is exaggerated for illustration, as a milliradian is much smaller in reality).

Use of the milliradian is practical because it is concerned with small angles, and when using radians the small angle approximation shows that the angle approximates to the sine of the angle, that is . This allows a user to dispense with trigonometry and use simple ratios to determine size and distance with high accuracy for rifle and short distance artillery calculations by using the handy property of subtension: One mrad approximately subtends one meter at a distance of one thousand meters.
More in detail, because , instead of finding the angular distance denoted by θ (Greek letter theta) by using the tangent function
- ,
one can instead make a good approximation by using the definition of a radian and the simplified formula:
Since a radian is mathematically defined as the angle formed when the length of a circular arc equals the radius of the circle, a milliradian, is the angle formed when the length of a circular arc equals 1/1000 of the radius of the circle. Just like the radian, the milliradian is dimensionless, but unlike the radian where the same unit must be used for radius and arc length, the milliradian needs to have a ratio between the units where the subtension is a thousandth of the radius when using the simplified formula.
Approximation error
The approximation error by using the simplified linear formula will increase as the angle increases. For example, a
- 3.3×10% (or 3.3 parts per billion) error for an angle of 0.1 mrad, for instance by assuming 0.1 mrad equals 1 cm at 100 m
- 0.03% error for 30 mrad, i.e. assuming 30 mrad equals 30 m at 1 km
- 2.9% error for 300 mrad, i.e. assuming 300 mrad equals 300 m at 1 km
| Calculation of percentage error for mrad |
|---|
|
|
The approximation using mrad is more precise than using another common system where 1′ (minute of arc) is approximated as 1 inch at 100 yards, where comparably there is a:
- 4.72% error by assuming that an angle of 1′ equals 1 inch at 100 yd
- 4.75% error for 100′, i.e. assuming 100′ equals 100 in at 100 yd
- 7.36% error for 1000′, i.e. assuming 1000′ equals 1000 inches at 100 yd
| Calculation of percentage error for arcminutes |
|---|
|
where |
Sight adjustment

Milliradian adjustment is commonly used as a unit for clicks in the mechanical adjustment knobs (turrets) of iron and scope sights both in the military and civilian shooting sports. New shooters are often explained the principle of subtensions in order to understand that a milliradian is an angular measurement. Subtension is the physical amount of space covered by an angle and varies with distance. Thus, the subtension corresponding to a mrad (either in an mrad reticle or in mrad adjustments) varies with range. Knowing subtensions at different ranges can be useful for sighting in a firearm if there is no optic with an mrad reticle available, but involves mathematical calculations, and is therefore not used very much in practical applications. Subtensions always change with distance, but an mrad (as observed through an optic) is always an mrad regardless of distance. Therefore, ballistic tables and shot corrections are given in mrads, thereby avoiding the need for mathematical calculations.
If a rifle scope has mrad markings in the reticle (or there is a spotting scope with an mrad reticle available), the reticle can be used to measure how many mrads to correct a shot even without knowing the shooting distance. For instance, assuming a precise shot fired by an experienced shooter missed the target by 0.8 mrad as seen through an optic, and the firearm sight has 0.1 mrad adjustments, the shooter must then dial 8 clicks on the scope to hit the same target under the same conditions.
Common click values
- General purpose scopes
- Gradations (clicks) of 1/4′, 1/10 mrad and 1/2′ are used in general purpose sights for hunting, target and long range shooting at varied distances. The click values are fine enough to get dialed in for most target shooting and coarse enough to keep the number of clicks down when dialing.
- Speciality scopes
- 0.25/10 mrad, 1/8′ and 0.5/10 mrad are used in speciality scope sights for extreme precision at fixed target ranges such as benchrest shooting. Some specialty iron sights used in ISSF 10 m, 50 m and 300 meter rifle come with adjustments in either 0.5/10 mrad or 0.25/10 mrad. The small adjustment value means these sights can be adjusted in very small increments. These fine adjustments are however not very well suited for dialing between varied distances such as in field shooting because of the high number of clicks that will be required to move the line of sight, making it easier to lose track of the number of clicks than in scopes with larger click adjustments. For instance to move the line of sight 0.4 mrad, a 0.1 mrad scope must be adjusted 4 clicks, while comparably a 0.05 mrad and 0.025 mrad scope must be adjusted 8 and 16 clicks respectively.
- Others
- 1.5/10 mrad and 2/10 mrad can be found in some short range sights, mostly with capped turrets, but are not very widely used.
Subtensions at different distances
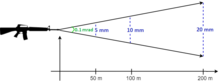
Subtension refers to the length between two points on a target, and is usually given in either centimeters, millimeters or inches. Since an mrad is an angular measurement, the subtension covered by a given angle (angular distance or angular diameter) increases with viewing distance to the target. For instance the same angle of 0.1 mrad will subtend 10 mm at 100 meters, 20 mm at 200 meters, etc., or similarly 0.39 inches at 100 m, 0.78 inches at 200 m, etc.
Subtensions in mrad based optics are particularly useful together with target sizes and shooting distances in metric units. The most common scope adjustment increment in mrad based rifle scopes is 0.1 mrad, which are sometimes called "one centimeter clicks" since 0.1 mrad equals exactly 1 cm at 100 meters, 2 cm at 200 meters, etc. Similarly, an adjustment click on a scope with 0.2 mrad adjustment will move the point of bullet impact 2 cm at 100 m and 4 cm at 200 m, etc.
When using a scope with both mrad adjustment and a reticle with mrad markings (called a mrad/mrad scope), the shooter can spot his own bullet impact and easily correct the sight if needed. If the shot was a miss, the mrad reticle can simply be used as a "ruler" to count the number of milliradians the shot was off target. The number of milliradians to correct is then multiplied by ten if the scope has 0.1 mrad adjustments. If for instance the shot was 0.6 mrad to the right of the target, 6 clicks will be needed to adjust the sight. This way there is no need for math, conversions, knowledge of target size or distance. This is true for a first focal plane scope at all magnifications, but a variable second focal plane must be set to a given magnification (usually its maximum magnification) for any mrad scales to be correct.
When using a scope with mrad adjustments, but without mrad markings in the reticle (i.e. a standard duplex cross-hair on a hunting or benchrest scope), sight correction for a known target subtension and known range can be calculated by the following formula, which utilizes the fact that an adjustment of 1 mrad changes the impact as many millimeters as there are meters:
For instance:
- 20 mm/50 m = 0.4 mrad, or 4 clicks with a 1/10 mrad adjustment scope.
- 50 mm/1000 m = 0.05 mrad, or 1 click with a 0.05 mrad adjustment scope.
In firearm optics, where 0.1 mrad per click is the most common mrad based adjustment value, another common rule of thumb is that an adjustment of 1/10 mrad changes the impact as many centimeters as there are hundreds of meters. In other words, 1 cm at 100 meters, 2.25 cm at 225 meters, 0.5 cm at 50 meters, etc. See the table below
| Range | Subtension | |||
|---|---|---|---|---|
| 1 mrad | 1/10 mrad | |||
| 100 m | 100 mm | 10 cm | 10 mm | 1 cm |
| 200 m | 200 mm | 20 cm | 20 mm | 2 cm |
| 300 m | 300 mm | 30 cm | 30 mm | 3 cm |
| 400 m | 400 mm | 40 cm | 40 mm | 4 cm |
| 500 m | 500 mm | 50 cm | 50 mm | 5 cm |
| 600 m | 600 mm | 60 cm | 60 mm | 6 cm |
| 700 m | 700 mm | 70 cm | 70 mm | 7 cm |
| 800 m | 800 mm | 80 cm | 80 mm | 8 cm |
| 900 m | 900 mm | 90 cm | 90 mm | 9 cm |
| 1000 m | 1000 mm | 100 cm | 100 mm | 10 cm |
Adjustment range and base tilt

The horizontal and vertical adjustment range of a firearm sight is often advertised by the manufacturer using mrads. For instance a rifle scope may be advertised as having a vertical adjustment range of 20 mrad, which means that by turning the turret the bullet impact can be moved a total of 20 meters at 1000 meters (or 2 m at 100 m, 4 m at 200 m, 6 m at 300 m etc.). The horizontal and vertical adjustment ranges can be different for a particular sight, for instance a scope may have 20 mrad vertical and 10 mrad horizontal adjustment. Elevation differ between models, but about 10–11 mrad are common in hunting scopes, while scopes made for long range shooting usually have an adjustment range of 20–30 mrad (70–100 moa).
Sights can either be mounted in neutral or tilted mounts. In a neutral mount (also known as "flat base" or non-tilted mount) the sight will point reasonably parallel to the barrel, and be close to a zero at 100 meters (about 1 mrad low depending on rifle and caliber). After zeroing at 100 meters the sight will thereafter always have to be adjusted upwards to compensate for bullet drop at longer ranges, and therefore the adjustment below zero will never be used. This means that when using a neutral mount only about half of the scope's total elevation will be usable for shooting at longer ranges:
In most regular sport and hunting rifles (except for in long range shooting), sights are usually mounted in neutral mounts. This is done because the optical quality of the scope is best in the middle of its adjustment range, and only being able to use half of the adjustment range to compensate for bullet drop is seldom a problem at short and medium range shooting.
However, in long range shooting tilted scope mounts are common since it is very important to have enough vertical adjustment to compensate for the bullet drop at longer distances. For this purpose scope mounts are sold with varying degrees of tilt, but some common values are:
- 3 mrad, which equals 3 m at 1000 m (or 0.3 m at 100 m)
- 6 mrad, which equals 6 m at 1000 m (or 0.6 m at 100 m)
- 9 mrad, which equals 9 m at 1000 m (or 0.9 m at 100 m)
With a tilted mount the maximum usable scope elevation can be found by:
The adjustment range needed to shoot at a certain distance varies with firearm, caliber and load. For example, with a certain .308 load and firearm combination, the bullet may drop 13 mrad at 1000 meters (13 meters). To be able to reach out, one could either:
- Use a scope with 26 mrad of adjustment in a neutral mount, to get a usable adjustment of 26 mrad/2 = 13 mrad
- Use a scope with 14 mrad of adjustment and a 6 mrad tilted mount to achieve a maximum adjustment of 14 mrad/2 + 6 = 13 mrad
Shot groupings
Main article: Shot grouping
 Two shot groupings obtained with different firearms at different distances.
Two shot groupings obtained with different firearms at different distances. The group on the left measures about 13 mm and was fired at about 45 meters, which equals 13 mm/45 m = 0.289 mrad.
The group on the right measures about 7 mm and was fired at about 90 meters, which equals 7 mm/90 m = 0.078 mrad.
A shot grouping is the spread of multiple shots on a target, taken in one shooting session. The group size on target in milliradians can be obtained by measuring the spread of the rounds on target in millimeters with a caliper and dividing by the shooting distance in meters. This way, using milliradians, one can easily compare shot groupings or target difficulties at different shooting distances.
If the firearm is attached in a fixed mount and aimed at a target, the shot grouping measures the firearm's mechanical precision and the uniformity of the ammunition. When the firearm also is held by a shooter, the shot grouping partly measures the precision of the firearm and ammunition, and partly the shooter's consistency and skill. Often the shooters' skill is the most important element towards achieving a tight shot grouping, especially when competitors are using the same match grade firearms and ammunition.
Range estimation with mrad reticles


Many telescopic sights used on rifles have reticles that are marked in mrad. This can either be accomplished with lines or dots, and the latter is generally called mil-dots. The mrad reticle serves two purposes, range estimation and trajectory correction.
With a mrad reticle-equipped scope the distance to an object can be estimated with a fair degree of accuracy by a trained user by determining how many milliradians an object of known size subtends. Once the distance is known, the drop of the bullet at that range (see external ballistics), converted back into milliradians, can be used to adjust the aiming point. Generally mrad-reticle scopes have both horizontal and vertical crosshairs marked; the horizontal and vertical marks are used for range estimation and the vertical marks for bullet drop compensation. Trained users, however, can also use the horizontal dots to compensate for bullet drift due to wind. Milliradian-reticle-equipped scopes are well suited for long shots under uncertain conditions, such as those encountered by military and law enforcement snipers, varmint hunters and other field shooters. These riflemen must be able to aim at varying targets at unknown (sometimes long) distances, so accurate compensation for bullet drop is required.

Angle can be used for either calculating target size or range if one of them is known. Where the range is known the angle will give the size, where the size is known then the range is given. When out in the field angle can be measured approximately by using calibrated optics or roughly using one's fingers and hands. With an outstretched arm one finger is approximately 30 mrad wide, a fist 150 mrad and a spread hand 300 mrad.
Milliradian reticles often have dots or marks with a spacing of 1 mrad in between, but graduations can also be finer and coarser (i.e. 0.8 or 1.2 mrad).
Units for target size and range
While a radian is defined as an angle on the unit circle where the arc and radius have equal length, a milliradian is defined as the angle where the arc length is one thousandth of the radius. Therefore, when using milliradians for range estimation, the unit used for target distance needs to be thousand times as large as the unit used for target size. Metric units are particularly useful in conjunction with a mrad reticle because the mental arithmetic is much simpler with decimal units, thereby requiring less mental calculation in the field. Using the range estimation formula with the units meters for range and millimeters for target size it is just a matter of moving decimals and do the division, without the need of multiplication with additional constants, thus producing fewer rounding errors.
| Derivation of the range formula |
|---|
These relations can easily be derived by looking at the units:
and vice versa
|
The same holds true for calculating target distance in kilometers using target size in meters.
Also, in general the same unit can be used for subtension and range if multiplied with a factor of thousand, i.e.
If using the imperial units yards for distance and inches for target size, one has to multiply by a factor of 1000⁄36 ≈ 27.78, since there are 36 inches in one yard.
If using the metric unit meters for distance and the imperial unit inches for target size, one has to multiply by a factor of 25.4, since one inch is defined as 25.4 millimeters.
Practical examples

Land Rovers are about 3 to 4 m long, "smaller tank" or APC/MICV at about 6 m (e.g. T-34 or BMP) and about 10 m for a "big tank." From the front a Land Rover is about 1.5 m wide, most tanks around 3–3.5 m. So a SWB Land Rover from the side is one finger wide at about 100 m. A modern tank would have to be at a bit over 300 m.
If, for instance a target known to be 1.5 m in height (1500 mm) is measured to 2.8 mrad in the reticle, the range can be estimated to:
So if the above-mentioned 6 m long BMP (6000 mm) is viewed at 6 mrad its distance is 1000 m, and if the angle of view is twice as large (12 mrad) the distance is half as much, 500 m.
When used with some riflescopes of variable objective magnification and fixed reticle magnification (where the reticle is in the second focal plane), the formula can be modified to:
Where mag is scope magnification. However, a user should verify this with their individual scope since some are not calibrated at 10× . As above target distance and target size can be given in any two units of length with a ratio of 1000:1.
Mixing mrad and minutes of arc
It is possible to purchase rifle scopes with a mrad reticle and minute-of-arc turrets, but it is general consensus that such mixing should be avoided. It is preferred to either have both a mrad reticle and mrad adjustment (mrad/mrad), or a minute-of-arc reticle and minute-of-arc adjustment to utilize the strength of each system. Then the shooter can know exactly how many clicks to correct based on what he sees in the reticle.
If using a mixed system scope that has a mrad reticle and arcminute adjustment, one way to make use of the reticle for shot corrections is to exploit that 14′ approximately equals 4 mrad, and thereby multiplying an observed corrections in mrad by a fraction of 14/4 when adjusting the turrets.
Conversion table for firearms

In the table below conversions from mrad to metric values are exact (e.g. 0.1 mrad equals exactly 1 cm at 100 meters), while conversions of minutes of arc to both metric and imperial values are approximate.
| Increment, or click |
(mins of arc) |
(milli- radians) |
At 100 m | At 100 yd | ||
|---|---|---|---|---|---|---|
| (mm) | (cm) | (in) | (in) | |||
| 1⁄12′ | 0.083′ | 0.024 mrad | 2.42 mm | 0.242 cm | 0.0958 in | 0.087 in |
| 0.25⁄10 mrad | 0.086′ | 0.025 mrad | 2.5 mm | 0.25 cm | 0.0985 in | 0.09 in |
| 1⁄8′ | 0.125′ | 0.036 mrad | 3.64 mm | 0.36 cm | 0.144 in | 0.131 in |
| 1⁄6′ | 0.167′ | 0.0485 mrad | 4.85 mm | 0.485 cm | 0.192 in | 0.175 in |
| 0.5⁄10 mrad | 0.172′ | 0.05 mrad | 5 mm | 0.5 cm | 0.197 in | 0.18 in |
| 1⁄4′ | 0.25′ | 0.073 mrad | 7.27 mm | 0.73 cm | 0.29 in | 0.26 in |
| 1⁄10 mrad | 0.344′ | 0.1 mrad | 10 mm | 1 cm | 0.39 in | 0.36 in |
| 1⁄2′ | 0.5′ | 0.145 mrad | 14.54 mm | 1.45 cm | 0.57 in | 0.52 in |
| 1.5⁄10 mrad | 0.516′ | 0.15 mrad | 15 mm | 1.5 cm | 0.59 in | 0.54 in |
| 2⁄10 mrad | 0.688′ | 0.2 mrad | 20 mm | 2 cm | 0.79 in | 0.72 in |
| 1′ | 1.0′ | 0.291 mrad | 29.1 mm | 2.91 cm | 1.15 in | 1.047 in |
| 1 mrad | 3.438′ | 1 mrad | 100 mm | 10 cm | 3.9 in | 3.6 in |
- 0.1 mrad equals exactly 1 cm at 100 m
- 1 mrad ≈ 3.44′, so 1/10 mrad ≈ 1/3′
- 1′ ≈ 0.291 mrad (or 2.91 cm at 100 m, approximately 3 cm at 100 m)
Definitions for maps and artillery


Because of the definition of pi, in a circle with a diameter of one there are 2000 π milliradians (≈ 6283.185 mrad) per full turn. In other words, one real milliradian covers just under 1/6283 of the circumference of a circle, which is the definition used by telescopic rifle sight manufacturers in reticles for stadiametric rangefinding.
For maps and artillery, three rounded definitions are used which are close to the real definition, but more easily can be divided into parts. The different map and artillery definitions are sometimes referred to as "angular mils", and are:
- 1/6400 of a circle in NATO countries.
- 1/6000 of a circle in the former Soviet Union and Finland (Finland phasing out the standard in favour of the NATO standard).
- 1/6300 of a circle in Sweden. The Swedish term for this is streck, literally "line".
Reticles in some artillery sights are calibrated to the relevant artillery definition for that military, i.e. the Carl Zeiss OEM-2 artillery sight made in East Germany from 1969 to 1976 is calibrated for the eastern bloc 6000 mil circle.
Various symbols have been used to represent angular mils for compass use:
- mil, MIL and similar abbreviations are often used by militaries in the English speaking part of the world.
- ‰, called "artillery per milles" (German: Artilleriepromille), a symbol used by the Swiss Army.
- ¯, called "artillery line" (German: artilleristische Strich), a symbol used by the German Army (not to be confused with Compass Point (German: Nautischer Strich, 32 "nautical lines" per circle) which sometimes use the same symbol. However, the DIN standard (DIN 1301 part 3) is to use ¯ for artillery lines, and " for nautical lines.)
- ₥, called "thousandths" (French: millièmes), a symbol used on some older French compasses.
- (Finnish: piiru, Swedish: delstreck), a symbol used by the Finnish Defence Forces for the standard Warsaw Pact mil. Sometimes just marked as v if superscript is not available.
Conversion table for compasses
| Milliradian | NATO mil | Warsaw Pact Mil | Swedish streck | Turn | Degrees | Minute of arc | |
|---|---|---|---|---|---|---|---|
| 1 milliradian = | 1 | 1.018592 | 0.954930 | 1.002677 | 1⁄2000π | 9/50π ≈ 0.057296 | 54/5π ≈ 3.437747 |
| 1 NATO mil = | 0.981719 | 1 | 0.9375 | 0.984375 | 1⁄6400 | 0.05625 | 3.375 |
| 1 Warsaw Pact mil = | 1.047167 | 1.066667 | 1 | 1.05 | 1⁄6000 | 0.06 | 3.6 |
| 1 Swedish streck = | 0.997302 | 1.015873 | 0.952381 | 1 | 1⁄6300 | 0.057143 | 3.428572 |
| 1 Nautical line = | 196.349541 | 200 | 187.5 | 196.875 | 1⁄32 | 11.25 | 675 |
| 1 degree = | 50π/9 ≈ 17.452778 | 17.777778 | 16.666667 | 17.5 | 1⁄360 | 1 | 60 |
| 1 minute of arc = | 5π/54 ≈ 0.290880 | 0.296297 | 0.277778 | 0.291667 | 1⁄21600 | 0.016667 | 1 |
-
 A 360 degree and 6400 NATO mil compass rose.
A 360 degree and 6400 NATO mil compass rose.
-
 Swiss Army compass with 6400 ‰ ("artillery per milles")
Swiss Army compass with 6400 ‰ ("artillery per milles")
-
 US Army compass with scales both in 360 degrees and NATO 6400 mil
US Army compass with scales both in 360 degrees and NATO 6400 mil
-
 Soviet Army wrist compass with two (opposite) scales, 360 degrees clockwise and 6000 Soviet mil counterclockwise.
Soviet Army wrist compass with two (opposite) scales, 360 degrees clockwise and 6000 Soviet mil counterclockwise.
Use in artillery sights
Artillery uses angular measurement in gun laying, the azimuth between the gun and its target many kilometers away and the elevation angle of the barrel. This means that artillery uses mils to graduate indirect fire azimuth sights (called dial sights or panoramic telescopes), their associated instruments (directors or aiming circles), their elevation sights (clinometers or quadrants), together with their manual plotting devices, firing tables and fire control computers.
Artillery spotters typically use their calibrated binoculars to move fired projectiles' impact onto a target. Here they know the approximate range to the target and so can read off the angle (+ quick calculation) to give the left/right corrections in meters. A mil is a meter at a range of one thousand meters (for example, to move the impact of an artillery round 100 meters by a gun firing from 3 km away, it is necessary to shift the direction by 100/3 = 33.3 mils.)
Other scientific and technological uses
The milliradian (and other SI multiples) is also used in other fields of science and technology for describing small angles, i.e. measuring alignment, collimation, and beam divergence in optics, and accelerometers and gyroscopes in inertial navigation systems.
See also
- Scandinavian mile, a unit of length common in Norway and Sweden, but not Denmark, today standardised as 10 kilometers.
- Thousandth of an inch, an inch-based unit often called a thou or a mil.
- Circular mil, a unit of area, equal to the area of a circle with a diameter of one thousandth of an inch.
- Square mil, a unit of area, equal to the area of a square with sides of length of one thousandth of an inch.
Footnotes
- Sweden (and Finland) have not been part of NATO nor the Warsaw Pact. However that Sweden has changed its map grid systems and angular measurement to those used by NATO, so the "streck" measurement unit is obsolete.
References
- "How to use milliradian-adjustable scopes". Outdoor Hub. 14 July 2011.
- Renaud, Hugues (31 May 2002). Dictionnaire historique de la Suisse. Fonds, AV Laussane.
Dapples: ... Charles-Marc (1837-1920), ingénieur, professeur à l'université de Lausanne, municipal à Lausanne, est l'inventeur de l'unité appelée "millième" pour mesurer les angles dans le tir d'artillerie. Une branche de la famille s'est fixée à Gênes à la fin du XVIIIe s.
- "Calculation of approximation error for 0.1 mrad". Wolfram Alpha.
- "Calculation of approximation error for 30 mrad". Wolfram Alpha.
- "Calculation of approximation error for 300 mrad". Wolfram Alpha.
- "Calculation of approximation error for 1′". Wolfram Alpha.
- "Calculation of approximation error for 100′". Wolfram Alpha.
- "Calculation of approximation error for 1000′". Wolfram Alpha.
- "Divisions GB". Online Compass Museum. Compassipedia.
- Taistelijan Opas 2013 (PDF) (in Finnish). Army Command (Finland). ISBN 978-951-25-2485-3. Archived (PDF) from the original on 5 May 2016. Retrieved 18 May 2019.
- "Suunnistus: Piiru" (in Finnish). Archived from the original on 18 May 2019. Retrieved 18 May 2019.
- "Optical Beam Alignment Meter". Opto-Mechanical Products Catalog. Light Test & Measurement Instruments. Vilnius, LT: Standa.
- "The mirror alignment and control system for CT5" (PDF). The H.E.S.S. experiment. Geneva, CH: CERN.
- "Focusing and Collimating". Newport. Technical Note.
Photonics solutions for extending the frontiers of science
- "beam divergence". Encyclopedia of Laser Physics and Technology.
- Groves, Paul D. (2013). Principles of GNSS, Inertial, and Multisensor Integrated Navigation Systems (Second ed.). ISBN 9781608070053.
- Nebylov, Alexander V.; Watson, Joseph (2016). Aerospace Navigation Systems. John Wiley & Sons. ISBN 9781119163060.
External links
- "angles". convertworld.com.
- Simeone, Robert J. "Mils / MOA & the range estimation equations". scribd.com.
- "Compassipedia". The Online Compass Museum.
 . This allows a user to dispense with
. This allows a user to dispense with  , instead of finding the
, instead of finding the  ,
,













